Das Tiefpassfilter filtert die höheren Frequenzen als die Grenzfrequenz ![]() heraus und lässt die Tieferen durch.
heraus und lässt die Tieferen durch.

Die Übertragungsfunktion eines digitalen Tiefpassfilters 2. Ordnung kann als
(1) ![]()
beschrieben werden.
Ermittlung der Koeffizienten für das Biquad-filter
Nach der bilinearen Transformation erhält man
(2) 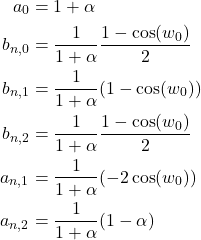
wobei
(3) 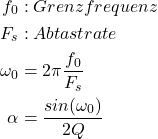
Implementierung
Somit erhält man alle Koeffizienten, die man für die Implementierung braucht. Die Implementierung der Koeffizientenberechnung würde folgendermaßen aussehen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
//Deklaration double A,w0,cosw0,sinw0,alpha,a0; //Hilfsvariablen A=pow(10,gain/40); w0=2*PI*(f0/FS); cosw0=cos(w0); sinw0=sin(w0); alpha=sinw0/(2*Q); //Normalisierungsparameter a0_inv=1/(1+alpha); //Koeffizientenberechnung bn0=(float)((1-cosw0)*0.5*a0_inv); bn1=(float)((1-cosw0)*a0_inv); bn2=bn0; an1=(float)((-2*cosw0)*a0_inv); an2=(float)((1-alpha)*a0_inv); |
Am Code lassen sich manche Optimierungen erkennen.
- Mehrmals vorkommende Variablen sind vorberechnet (z.B. trigonometrische Funktionen)
- Anstatt jedes mal durch
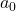 zu teilen, wird mit inversem (ein mal vorberechneten) Wert
zu teilen, wird mit inversem (ein mal vorberechneten) Wert 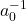 multipliziert, da Multiplikation günstiger ist als Division für viele CPUs.
multipliziert, da Multiplikation günstiger ist als Division für viele CPUs. - Die Berechnungen erfolgen mit Gleitkommezahlen doppelter Präzision (double) und wird am Ende auf Float gecastet. Der Grund: Trigonometrischen Funktionen mit Single-Präzision (float) kann zu erheblichen numerischen Fehlern und dadurch zu unerwünschten Ergebnissen bzw. Instabilität führen.
- Der Code ist optimiert für die Hardware-FPU von Cortex-M7 Mikroprozessor.

Schreibe einen Kommentar