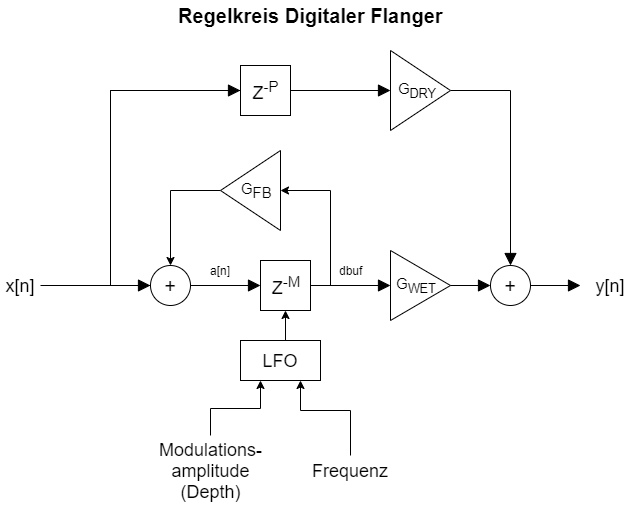
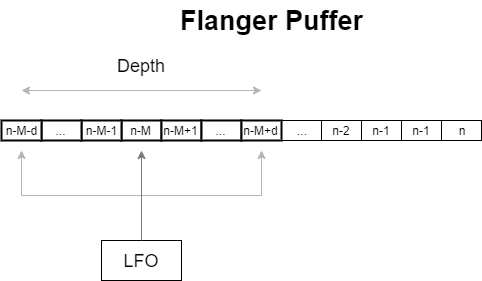
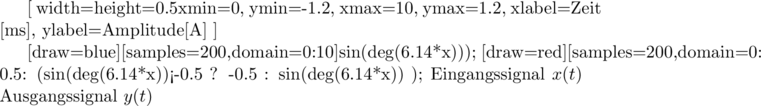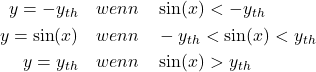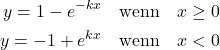Die Dynamikkompression (engl. Dynamic range compression) ist ein Prozess, der die Dynamik komprimiert bzw. reduziert. Das wird gemacht, indem die lauten Bereiche, die einen Schwellwert überschreiten, leiser gemacht werden, während die leiseren Bereiche unreduziert passieren. Die Charakteristik der Kompression lässt sich am Besten in einer Dynamikkurve darstellen, die die Beziehung zwischen der Einganglautstärke und Ausgangslautstärke beschreibt.
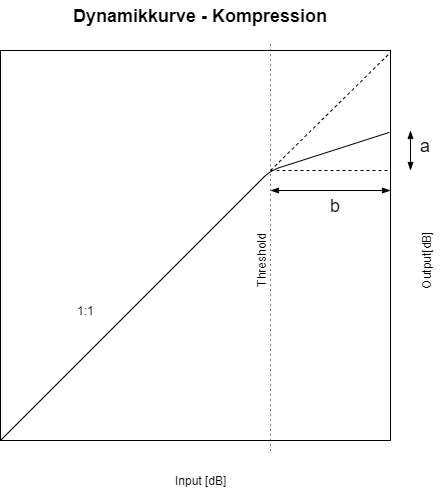
Die Steigung ![]() beschreibt die Kompressionsrate, mit der das Signal abgeschwächt wird. Dies greift ab dem Überschreiten eines Threshold-Werts.
beschreibt die Kompressionsrate, mit der das Signal abgeschwächt wird. Dies greift ab dem Überschreiten eines Threshold-Werts.
Technische Beschreibung
Das Herzstück eines Kompressors ist ein spannungskontrollierter Verstärker (VCA). Im analogen Design, wird das mit komplexen Schaltungen realisiert. In der Digitaltechnik ist dies ein simpler Verstärkungsfaktor, mit dem das Signal multipliziert wird. In analoger Welt kann der VCA u. a. mit
- Optokopplern (optische Kompressor)
- diskreten Transistorschaltungen
- integrierten Schaltkreisen
realisiert werden.
Der Verstärkungsfaktor wird in einem parallelen Pfad berechnet. Der parallele Pfad besteht aus einem Lautstärkendetektor (in der Regel realisiert mit Effektivleistung, RMS) und einer Logik, die die Reduktion aus der Lautstärke berechnet (Gain computer).
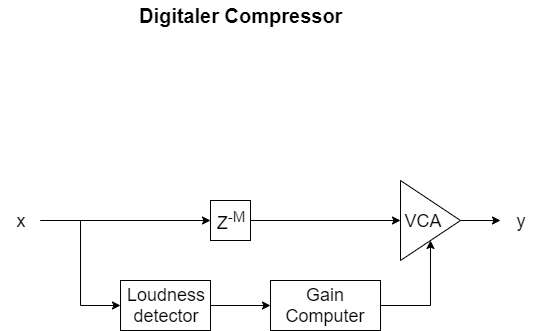
Loudness detector
Einer der wichtigsten Bestandteile einer Kompression ist die Berechnung der Lautstärke, Hier wird kontinuierlich ermittelt, wie hoch die empfundene Lautstärke ist. Gängigste Methode dafür ist der Effektivwert als quadratischer Mittelwert des relevanten Sampleabschnitts.
(1) 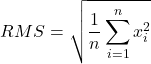
Der RMS-Wert dient als Eingang für den Gain-Computer. Der Gain-Computer berechnet daraus die Verstärkung, die dem Signal appliziert werden soll. Es appliziert die Dynamikkurve, s. oben.
Parameter
Folgende Kontrollparameter sind für einen Kompressor Effekt üblich:
Input gain
Die Eingangsverstärkung wird auf das Eingangssignal appliziert, um das Signalniveau in einen gewünschten Platz in der Dynamikkurve zu platzieren. Alternativ kann man auch Threshold verschieben.
Threshold
Der Threshold (dt. für Schranke/Grenze) ist der Grenzwert, ab dessen Überschreitung eine Gain-Reduktion erfolgt, s. Diagramm.
Kompressionsrate
Sie beschreibt die Stärke der Gain-Reduktion nach Threshold, in der Dynamikkurve ist dies als Tangenzwert ![]() gezeigt.
gezeigt.
Ab einem Wert von 60:1 wird von einem Limiter gesprochen.
Make-Up Gain
Der Gain-Computer appliziert eine Gain-Reduktion. Das bedeutet, die gesamte Lautstärke des Signals sinkt. Um das ältere Lautstärkenniveau zu erreichen, wird ein Make-Up Gain am Ausgang appliziert.
Soft-Knee / Hard-Knee
Ab dem Threshold ändert sich die Verstärkung, die man appliziert. Dieser Übergang, der in der Dynamikkurve oben scharf gezeichnet wurde, kann auch mild erfolgen. So dass die Gain-Reduktion langsam eintritt.
Attack
Der Attack-Wert bestimmt, wann die Gain-Reduktion nach einer Überschreitung eintreten soll. Sie liegt im Bereich von 5 bis 250 ms.
Release
Der Release-Wert bestimmt, wann nach einer Unterschreitung des Tresholds die Gain-Reduktion wieder aussetzen soll. Sie liegt üblicherweise im Bereich von 5 bis 100ms.
Analoge Implementierung
Bei Flex 500 wurde ein Kompressor auf Basis des integrierten Schaltkreises THAT4301 von THAT Corporation eingesetzt. Dieser beinhaltet
- 1x VCA
- 1x Loudness (RMS) detector
- 3x Opamps
und somit alles, was man für eine grundlegende Kompressorimplementierung braucht. Die Applikation und die Dimensionierung der externen Komponenten können dem Datenblatt entnommen werden.
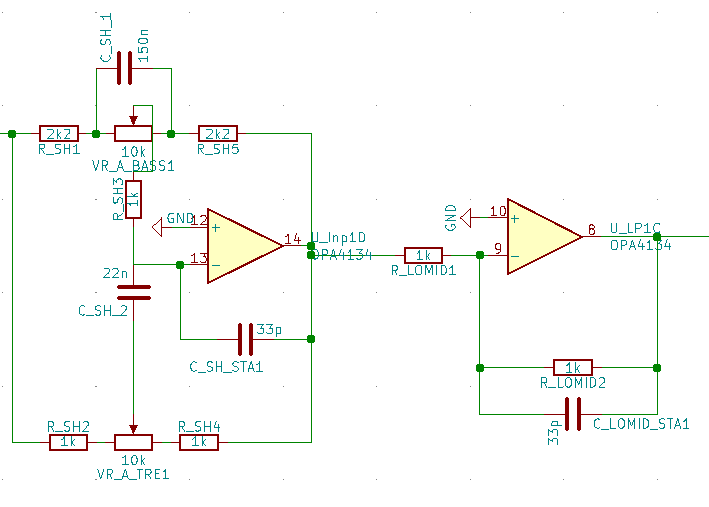
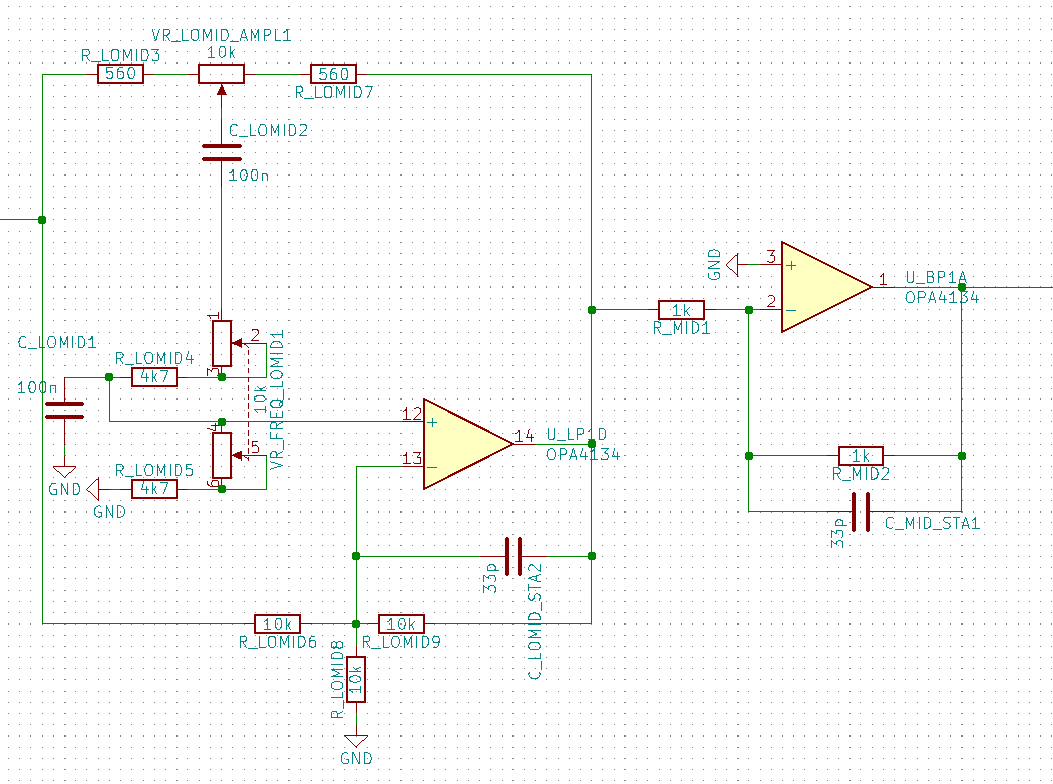
Die Applikation für den Flex 500 sieht folgendermaßen aus:
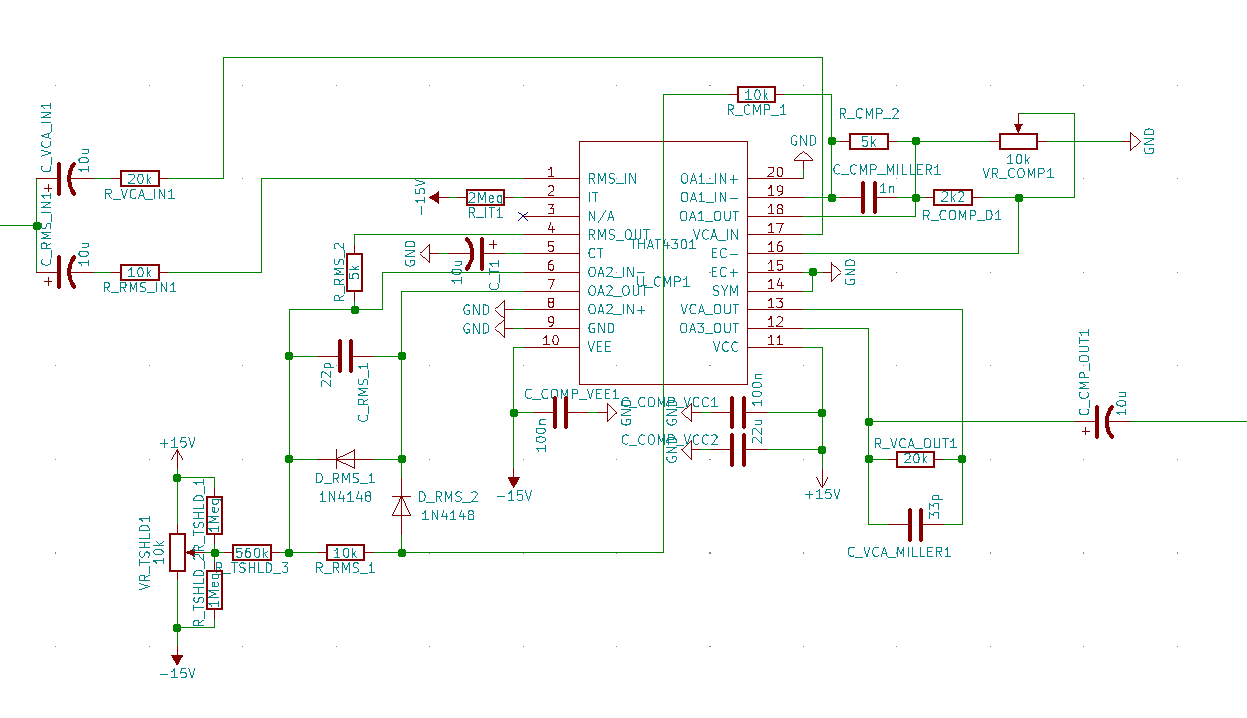
Zudem existiert ein SPICE-Modell für den IC THAT4301, sodass man die Schaltung auch simulieren kann.
Kompressor Simulationsmodell für LTSpice herunterladen
Die gesamte KiCAD-Schaltung und das PCB Design ist verfügbar