Wie im vorherigen Teil erwähnt, kann die Bewegung eines Mehrkörpersystems, in diesem Fall Roboter, mit Hilfe der bewegten Koordinaten Systeme leichter beschreiben. In dem Sonderfall der Starrkörper, lässt sich auch die Bewegung eines Körpers vollständig mit einem bewegten Koordinatensystem beschrieben.

Ein bewegtes Koordinatensystems K(t) bezüglich des Inertialsystems I wird mit einem 3\times1 Ortsvektor und einem 3\times3 Drehtensor beschrieben. Hierzu gelten die Transformationsgesetze der Vektoren und Matrizen. Für die Transformation eines Vektors w(t) gilt

(1)   \begin{equation*} _I\mathbf{w}(t)=_I\mathbf{r}_{IK}(t)+\mathbf{D}_{IK}(t) _K\mathbf{w}(t) \end{equation*}

wobei \mathbf{D}_{IK} der Drehtensor, der die Drehung des Koordinatensystems K(t) bezüglich des Koordinatensystems I beschreibt und der Vektor _I\mathbf{r}_{IK}(t) der Ortsvektor des Ursprungspunkts des Koordinatensystems K bezüglich des Koordinatensystems I ist.

Im allgemeinen Fall kann die Deformation eines flexiblen Körpers bezüglich eines bewegten Koordinatensystems beschrieben werden. Die Bewegung des diskreten Punktes _B\zeta eines Körpers mit körperfestem Bezugssystem B kann bezüglich des Inertialsystems als

(2)   \begin{equation*} _I\mathbf{r}(\zeta,t)=_I\mathbf{r}_{IK}(t)+\mathbf{D}_{IK}(t) [_K\mathbf{r}_{KB}(t)+\mathbf{D}_{KB}(t) _B \mathbf{\zeta}] \end{equation*}

formuliert werden. Hierbei ist \mathbf{D}_{KB}(t) der Drehtensor des Koordinatensystems B bezüglich K. Die zeitabhängigen und -unabhängigen Koordinatensysteme können prinzipiell beliebig verschachtelt werden. Die Prinzip der bewegten Koordinatensysteme bzw. mehrere verschachtelte Koordinatensysteme können sowohl für die Beschreibung der kontinuumsmechanischen Phänomene wie flexibler Körper als auch für die Beschreibung mehrerer geketteter Starrkörper, wie z.B. mehrgelenkige Roboter verwendet werden. Zwischen den Koordinatensystemen kann vorwärts- und rücktransformiert werden. Ausführliche Beschreibungen und viele Praxisbeispiele darüber sind u.a. in Weber09 und LenarcicBajdStanisic13 zu finden.

In unserem konkreten Fall werden die bewegten Koordinatensysteme für die Bewegung des Roboters bezüglich eines Körperfesten Koordinatensystems und für den Sollpfad verwendet. Die Sensorik, die hierzu verwendet wird, misst Bewegung nach einer relativen Messprinzip, siehe BorensteinFeng94 und BorensteinFeng96. Das heißt die Bewegung und Orientierung des Roboters wird inkrementell, bezüglich des letzten Zustands eines bewegten Koordinatensystems gemessen.

Rendered by QuickLaTeX.com

Abbildung 1: Beschreibung der Kinematik mit Hilfe des bewegten KOS
Gemessen und konstruiert wird die differentielle Bewegung des Roboters. Diese wird bezüglich des bewegten Koordinatensystems G in der Abbildung 1 als _G\mathbf{r}^B gekennzeichnet. So kann der Lagevektor des Roboters bezüglich des Inertialsystems _I\mathbf{r}^B als

(3)   \begin{equation*} _I\mathbf{r}^B(t)=_I\mathbf{r}_{IG}(t)+\mathbf{D}_{IG}(t) _K\mathbf{r}^G(t) \end{equation*}

berechnet werden, wobei der Drehtensor \mathbf{D}_{IG}(t) als

(4)   \begin{equation*} \mathbf{D}_{IG}(t)=\begin{bmatrix} \cos(_I\gamma^G)(t) & -\sin(_I\gamma^G)(t) &0 \\ \sin(_I\gamma^G)(t) & \cos(_I\gamma^G)(t) & 0 \\ 0&0&1 \end{bmatrix} \end{equation*}

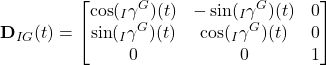
formuliert werden kann. Nach der Zeitdiskretisierung kann die Bewegung des Koordinatensystems G als

(5)   \begin{equation*} G(t+\Delta t):= B(t) = _I\tilde{\mathbf{r}}^B(t) \end{equation*}

beschrieben und programmiert werden, wobei

(6)   \begin{equation*} _I\tilde{\mathbf{r}}^B(t)=\begin{bmatrix} _I{\mathbf{r}}^B(t)\\ _I\mathbf{\omega}^B(t) \end{bmatrix} \end{equation*}

mit der Drehung des Koordinatensystems _I\mathbf{\omega}^B(t).

Somit hat man die Lage und die Orientierung des Roboters als die Bewegung eines Koordinatensystems wiedergegeben. Für den Sonderfall der Starrkörper, kann dies aber ein Hilfsmittel verwendet werden, siehe EberhardSchiehlen04.