Kontakte sind bekanntlicherweise nichtlineare Vorgänge. Zudem sind sie auch nicht-stetig. In meiner Diplomarbeit bei Bosch und ITM-Uni Stuttgart, wo ich Haft-, Gleitübergänge in einem Spindelantrieb modelliert habe, durfte ich mich mit der Theorie der Kontaktmechanik auseinandersetzen. Zudem gehörte auch die Theorie der Linearen Komplementaritätsprobleme (LCP).

Coulombsche Reibung ist ein bekanntes Reibungsmodell, das i.A. mit den Gleichungen

(1)   \begin{equation*} \begin{aligned} \dot{g}_T^l=0 & \Rightarrow -\mu_{0}^l \lambda_{N}^l \le \lambda_{T}^l \le \mu_{0}^l \lambda_{N}^l ~~ \text{ (Haften)}\\ \dot{g}_T^l\neq0 & \Rightarrow \lambda_{T}^l =-\mu_{0}^l \lambda_{N}^l~~ \text{ (Positives Gleiten)}\\ \end{aligned} \end{equation*}

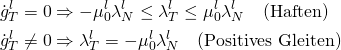
beschrieben werden kann, wenn man das Haft- und Gleitverhalten beschreiben will. Dabei ist \dot{g}_T die tangentiale Geschwindigkeit auf der Kontaktfläche. Wie man hier sieht, führt so eine Gleichung zu einem nichtlinearen und zudem einem komplemantären [ref]Ergänzung, ergänzend[/ref] Problem. Es lässt sich nicht mehr alleine mit gewöhnlichen Differentialgleichungen lösen.

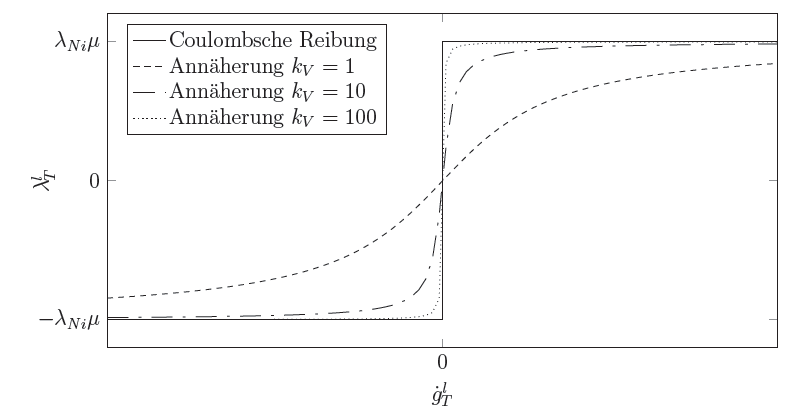
In der Praxis, wird meist Annäherungsansätze wie z.B.

(2)   \begin{equation*} \lambda_{T}^l=\cfrac{2}{\pi} \lambda_{N}^T \mu_{0}\ \text{arctan}(k_V \dot{g}_T^l)\text{.} \end{equation*}

mit Arcustangenz verwendet, die eine annäherungsweise Beschreibung des Kontakts ermöglichen.


Abbildung 1: Coulombsche Reibung und Annäherungsansätze gegenübergestellt

Wenn diese Annäherungsansätze nicht ausreichen, kann das nichtstetige Kontaktproblem mit Hilfe des LCP beschrieben werden. Im einfachsten Fall ist es ein idealer Normalkontakt, wie z.B. Stoß zweier Billardkugeln, siehe Abbildung 2.


Abbildung 2: Beschreibung des Normalkontakts

Dabei sind die Größen auf den Achsen die Größen, die sich „ergänzen“. Wenn g die Relativgeschwindigkeit beider Kugeln in Normalrichtung und \Delta_N die Normalkraft zwischen den Kugeln ist, bedeutet es: Wenn die Normalkraft größer als Null ist, dann beträgt die Relativgeschwindigkeit in Normalrichtung (Kontaktzustand) Null. Das gilt auch umgekehrt. Somit kann dieses Verhalten einfach als ein 1D-LCP Problem beschrieben werden.

Wenn man die Coulombsche Reibung beschreiben möchte, die nicht zufälligerweise der Standardform des LCP entspricht, muss das Verhalten der Coulombschen Reibung zerlegt werden, sodass es in die Standardform des LCP gebracht wird, siehe Abbildung 3.


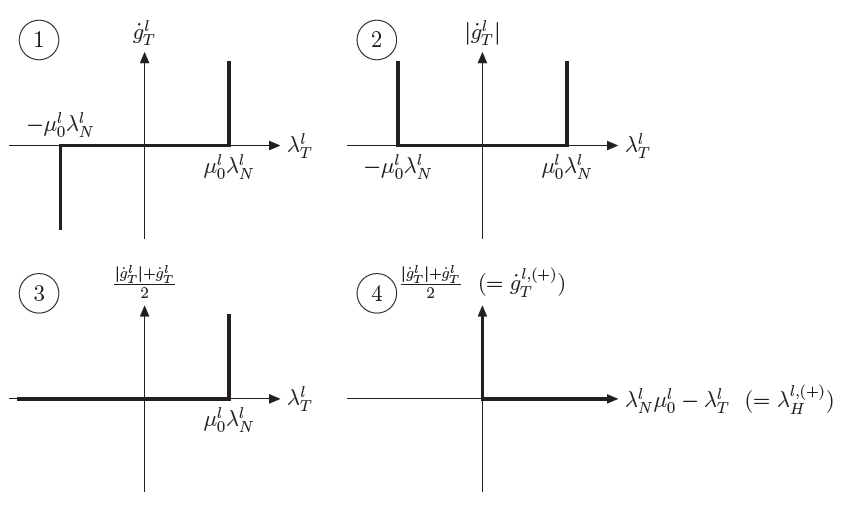
Abbildung 3: Beschreibung der Coulombschen Reibung

In diesem Fall bekommt man ein 2D-LCP. Die LCP Gleichungen sehen dabei folgendermaßen aus:

(3)   \begin{equation*} \begin{aligned} \underbrace{\ddot{\mathbf{g}}_{NH}}_{\boldsymbol{\gamma}}=\underbrace{(\mathbf{W}^T\cdot \mathbf{M}^{-1}\cdot \mathbf{W}_{NH})}_{\mathbf{A}}\cdot \underbrace{\boldsymbol{\lambda}}_{\boldsymbol{\chi}}+\underbrace{(\mathbf{W}^T\cdot \mathbf{M}^{-1}\cdot\mathbf{h}+ \mathbf{w})}_{\mathbf{b}}\\ \ddot{\mathbf{g}}_{NH}\geq 0, ~~\boldsymbol{\lambda}\geq 0,~~ \ddot{\mathbf{g}}_{NH}\cdot \boldsymbol{\lambda}=0 \text{,} \end{aligned} \end{equation*}

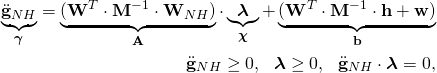
Die Beschreibung der vorkommenden Matrizen und die ausführliche Herleitung der LCP kann in meiner Diplomarbeit nachgelesen werden. Somit kann das LCP Problem mit einem LCP-Solver gelöst werden. Es hat praktisch die Bedeutung, dass beim Lösen der DGL in jedem Iterationsschritt das LCP-Problem gelöst werden muss, was ein zusätzlicher Rechenaufwand ist. Wie erwähnt, ermöglicht es die Beschreibung der nichtlinearen und nichtstetigen Vorgänge. Bei Fragen zu der Theorie oder Anwendung können Sie mich gerne kontaktieren.