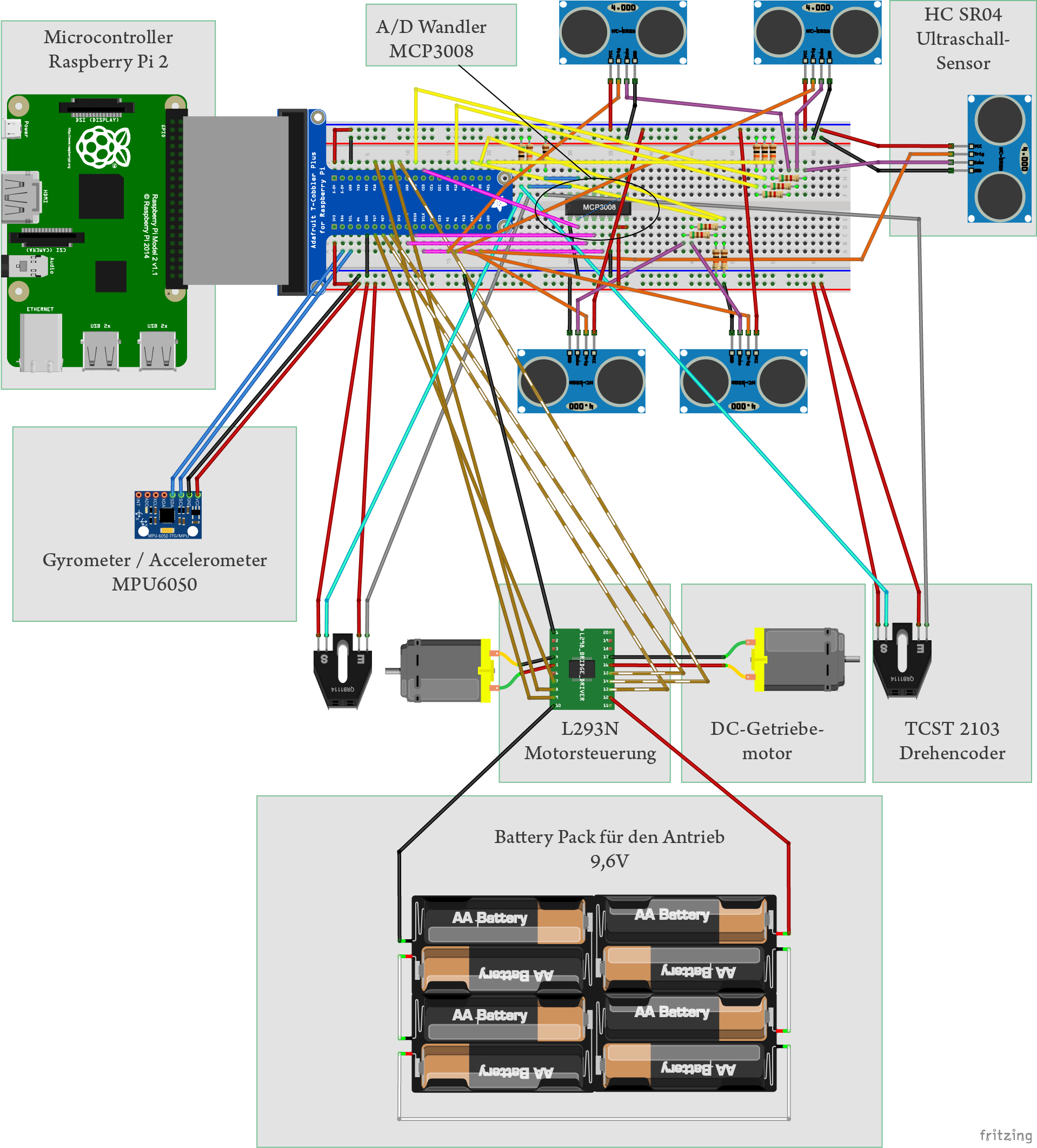
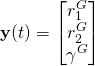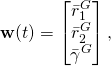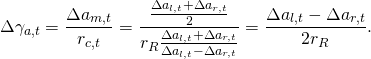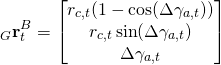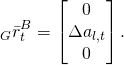Bei den SLAM-Robotern ist ein robustes Raumerfassungssystem von essenzieller Bedeutung. Bei den Robotern im Haushaltsbereich ist der Kostenfaktor des Raumerfassungssystems ein entscheidendes Kriterium. Die Ultraschall-Distanzmessung ist eine sehr interessante Möglichkeit, den Raum zu erfassen.
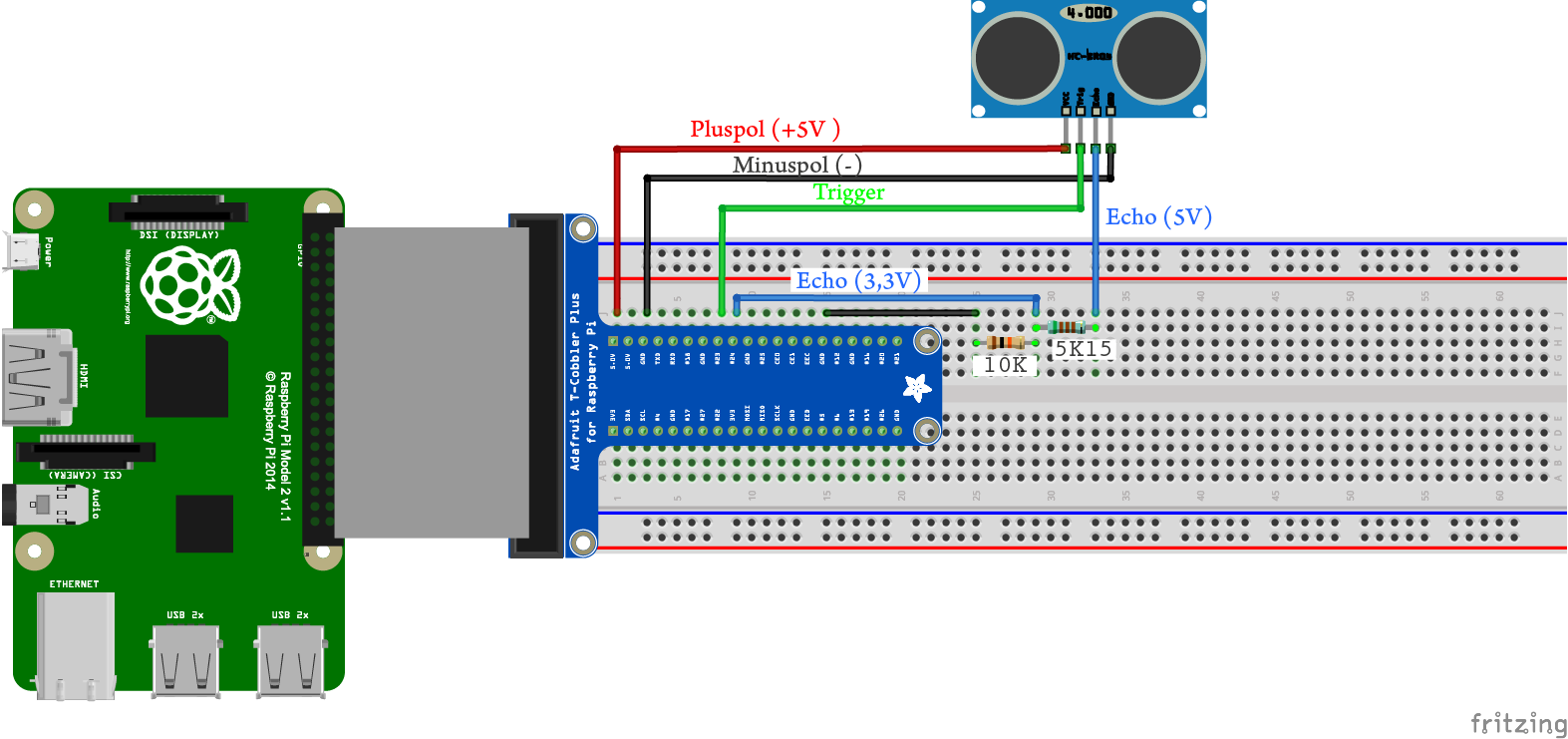
Ein analoges Ultraschallmodul für die Distanzmessung kostet bei großen Stückzahlen deutlich unter 1USD, da es eine einfache Elektronik hat und keine Präzisionsherstellung erfordert. Er kann die Objekte im Bereich ![]() erkennen. Die 1D-Messungen müssen, abhängig von der Roboterkonfiguration, ins Inertialsystem transformiert werden, um die 2D-Raumkarte zu erstellen. Die Schnittstelle HC-SR04 mit Raspberry Pi ist im Teil Schnittstelle Raspberry Pi und HC-SR04 erläutert.
erkennen. Die 1D-Messungen müssen, abhängig von der Roboterkonfiguration, ins Inertialsystem transformiert werden, um die 2D-Raumkarte zu erstellen. Die Schnittstelle HC-SR04 mit Raspberry Pi ist im Teil Schnittstelle Raspberry Pi und HC-SR04 erläutert.
Versuchsaufbau
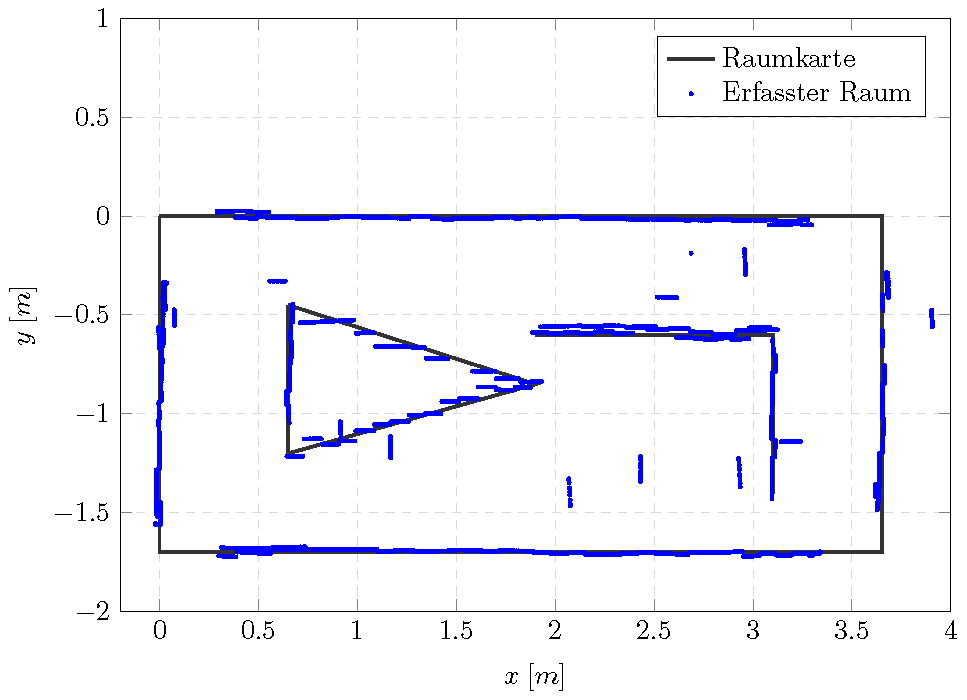
Der Mapping-Versuch mit Ultraschallsensoren wird in einem vorgemessenen, künstlichen Versuchsraum durchgeführt, siehe Abbildung 1.

Die Außenmaße des Messraums betragen ![]() . Der Roboter führt ein autonomes „Rechtsherumfahrt“ an den Wänden entlang und akquiritiert die 1D-Entfernungsdaten mit der aktuellen Roboterlage. Danach werden diese Daten ins Inertialsystem transformiert und es wird die Raumgeometrie erstellt. Erster Teil des Versuchs ist die einmalige Fahrt und die Interpretation der Messergebnisse. Im folgenden Video wird der Versuchsablauf vorgestellt.
. Der Roboter führt ein autonomes „Rechtsherumfahrt“ an den Wänden entlang und akquiritiert die 1D-Entfernungsdaten mit der aktuellen Roboterlage. Danach werden diese Daten ins Inertialsystem transformiert und es wird die Raumgeometrie erstellt. Erster Teil des Versuchs ist die einmalige Fahrt und die Interpretation der Messergebnisse. Im folgenden Video wird der Versuchsablauf vorgestellt.
Verarbeitung der Messdaten für die Erstellung der Raumkarte
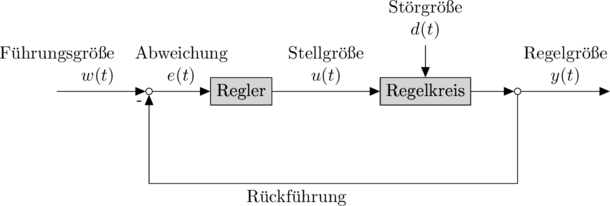
Erst müssen die 1-D Distanz-Messdaten aus den Sensoren in das Inertialsystem transformiert werden. Somit werden Punkte im Inertialsystem gewonnen, mit denen Abschätzungen über die die 2-D-Raumkarte gemacht werden können. Dabei werden die Wahrscheinlichkeiten bzw. die Varianzen der ermittelten Punkte berechnet, um die höchstwahrscheinliche Raumkarte abschätzen und nachkorrigieren zu können. Zu diesem Zweck dienen die Hilfsmittel wie vor allem Bayessches Theorem und Kalman Filter, mit denen die Wahrscheinlichkeiten der Messpunkte abgeschätzt und im Algorithmus abgespeichert werden, siehe SlamChoset, SlamSiegwarth.
Das Kalman-Filter kann für die Erstellung der Raumkarte mit mehreren Datenquellen verwendet werden (Sensor Fusion). In dem Quellcodverzeichnis befindet sich eine Beispiel-Implementierung für Kalman-Filter als Python-Code.
Tauglichkeit der Ultraschalltechnik als Haupt-Mappingsystem
Die Ultraschalltechnik ist bei zahlreichen Anwendungen eingesetzt auch als Distanzsensoren. Im Folgenden wird die Tauglichkeit dieser Technik für vorliegende Anwendung, der Indoor-SLAM-Roboter beurteilt.
Die Ultraschallsensoren charaktersieren sich in der Anwendung als Haupt-Mappingsystem mit folgenden Eigenschaften
– Großer Öffnungskegel der Ultraschallwellen
– Interferenz der Ultraschallwellen
– Ablenkung der Ultraschallwellen nach der Reflektion
– Geschwindigkeit der Ultraschallwellen / Abtastfrequenz
+ Niedriger Beschaffungspreis
Die Ultraschalltechnik bietet eine sehr günstige Möglichkeit, Distanzen bis zu ![]() zu messen. In Großserie kosten die Sensormodule deutlich unter 1USD.
zu messen. In Großserie kosten die Sensormodule deutlich unter 1USD.
– Großer Öffnungskegel der Wellen
Die Öffnungswinkel der Wellen aus Ultraschalltransmitter beträgt bei HC-SR04 ![]() bis über
bis über ![]() . Das ist eine fataler Nachteil dieser Technik gegenüber manchen anderen optischen Messmethoden. Die Auflösung sinkt deutlich mit der steigenden Entfernung. Die Varianz beträgt bei einer Entfernung von
. Das ist eine fataler Nachteil dieser Technik gegenüber manchen anderen optischen Messmethoden. Die Auflösung sinkt deutlich mit der steigenden Entfernung. Die Varianz beträgt bei einer Entfernung von ![]() demnach
demnach ![]() , die im 2D-Raum auf einem Kreisbogen des Schallkegels dargestellt werden kann.
, die im 2D-Raum auf einem Kreisbogen des Schallkegels dargestellt werden kann.
Diese Eigenschaft ist wiederrum vorteilhaft bei der Kollisionsverhinderung, wo ein breites Abtasten erforderlich ist. Daher stellt der Sensor eine gute Möglichkeit als Kollisionsverhinderungssensor dar.
– Interferenz der Ultraschallwellen
Das bei diesem Versuch verwendete Ultraschallsensormodul HC-SR04 ist ein nicht-konfigurierbares analoges Modul. Es schickt voreingestellt ![]() Sequenzen mit
Sequenzen mit ![]() . Somit können sich die Wellen, besonders bei nah-positionierten Sensoren, interferieren. Um diese Problematik umzugehen, müssen die Ultraschall-Impulse kodiert werden. Dies erfordert zusätzliche und ggf. teurere Elektronik
. Somit können sich die Wellen, besonders bei nah-positionierten Sensoren, interferieren. Um diese Problematik umzugehen, müssen die Ultraschall-Impulse kodiert werden. Dies erfordert zusätzliche und ggf. teurere Elektronik
– Ablenkung der Ultraschallwellen nach der Reflektion
Die Ultraschallwellen können an schrägen oder sonstigen ungünstigen reflektierenden Oberflächen bzw. Objekten abgelenkt werden, sodass die Wellen entweder nicht an den Empfänger zurückkehren oder abgeschwächt werden. In dem Versuch zeigten sich die Messdaten bei den Objekten, die dem Sensor schräger als ![]() stehen, als unbrauchbar. Dazu gehören auch verschiedene Kanten, die der Roboter schräg messen muss. Das stellt auch einen bedeutenden Nachteil dar, da die Räume und Objekte in der Praxis viel komplizierter und ungünstiger sein können.
stehen, als unbrauchbar. Dazu gehören auch verschiedene Kanten, die der Roboter schräg messen muss. Das stellt auch einen bedeutenden Nachteil dar, da die Räume und Objekte in der Praxis viel komplizierter und ungünstiger sein können.
– Geschwindigkeit der Ultraschallwellen / Abtastfrequenz
Die Geschwindigkeit der Ultraschallwellen beträgt in der Luft ![]() und stellt ebenso ein großes Hindernis in der Verwendung als Haupt-Mappingsystem dar, es eine maßgebende Beschränkung für die Abtastfrequenz ist. Im Versuch zeigten sich Abtastfrequenzen über
und stellt ebenso ein großes Hindernis in der Verwendung als Haupt-Mappingsystem dar, es eine maßgebende Beschränkung für die Abtastfrequenz ist. Im Versuch zeigten sich Abtastfrequenzen über ![]() als suboptimal, da die Messfehler bei niedrigeren Leerlaufzeiten drastisch zunehmen.
als suboptimal, da die Messfehler bei niedrigeren Leerlaufzeiten drastisch zunehmen.
Bei niedrigen Abtastfrequenzen muss das Beobachtermodell auch präziser definiert werden. Zwar bei einem bewegenden Roboter wird die Lage des Roboters beim Aussenden und Empfangen der Wellen unvernachlässigbar unterschiedlich sein. Dieses Phänomen muss im Modell ebenso berücksichtigt werden.
Zusammenfassung
Aufgrund seinem günstigen Beschaffungspreis ist Ultraschallsensor eine interessante Technik, um kurze Distanzen bis zu ![]() zu messen. Als zuverlässiges Haupt-Mappingsystem ist sie aufgrund der Breite und die Geschwindigkeit der Ultraschallwellen eher ungeeignet. Dennoch bietet er eine interessante Möglichkeit als Kollisionsverhinderungssensor an.
zu messen. Als zuverlässiges Haupt-Mappingsystem ist sie aufgrund der Breite und die Geschwindigkeit der Ultraschallwellen eher ungeeignet. Dennoch bietet er eine interessante Möglichkeit als Kollisionsverhinderungssensor an.
Ausblick
Die optischen Methoden, wie 1D-Laserentfernungsmessungen, die auf Triangulationsprinzip beruhen, sind für die 2D-Kartenerstellung geeigneter und ist der aktuelle Fokuspunkt der Entwicklung des Ropi. Ein weiterer Entwicklunsgegenstand ist der Mapping-Algorithmus auf der Basis von Kalman-Filter.